Coherent spectroscopy with a single antiproton spin

Precision measurements of the magnetic properties of simple systems stand as a powerful tool for investigating fundamental physics, enabling some of the most precise tests of symmetry violations. For instance, the experiments described in ref. ¹¹ used a ³He/¹²⁹Xe comagnetometer to place tight constraints on CPT-invariance-violating and Lorentz-invariance-violating parameters for neutrons¹². Incoherent studies of the magnetic properties of single electrons¹³ provide unparalleled tests of the Standard Model, while also setting constraints on the parameter space in which the dark photon could exist¹⁴. Meanwhile, direct measurements on ³He⁺ and ⁹Be⁺ ions have established the most precise absolute magnetometers so far¹⁵ and test multi-electron shielding factors¹⁶. Our experiments focus on antimatter-based magnetometry¹⁷ using cryogenic multi-Penning-trap systems. We have measured the proton (p) magnetic moment with a fractional accuracy of 300 ppt (ref. ¹⁸) and determined that of the antiproton ((bar{p})) with 1.5 ppb resolution⁸. These experiments are based on incoherent spin-projection measurements using the continuous Stern–Gerlach effect^19,20, combined with decoherent measurements of the Larmor ν_L and the cyclotron ν_c frequencies in the magnetic field B₀ = 1.945 T of our PT (ref. ²¹). The ratio of the measured frequencies gives the gyromagnetic g-factor g/2 = ν_L/ν_c. Decoherent Larmor resonance spectroscopy results in suppressed spin inversion and contributes to the broadening of the measured resonance lines, both of which diminish measurement resolution. Establishing coherent techniques to overcome these limitations is an exciting prospect and represents a key advancement towards establishing nuclear magnetic moment measurements at substantially improved resolution.

Here we demonstrate the coherent quantum transition spectroscopy of a single nuclear spin 1/2 particle—a single trapped antiproton. The measurements are carried out in the multi-Penning-trap system of the BASE collaboration¹⁷ at the Antiproton Decelerator (AD)/ELENA facility of CERN. By applying our unique two-particles/three-traps technique⁸, supported by our cooling trap (CT)²², we observe Rabi oscillations of a single (bar{p}) spin and achieve spin coherence times greater than 50 s. In line-shape scans, in which we vary an applied spin-flip radiofrequency ν_rf with respect to the Larmor frequency ({nu }_{{rm{L}}}=left(frac{{g}_{bar{p}}}{2}right)times {nu }_{{rm{c}}}), we obtain spin inversions greater than 70% and a full width at half maximum (FWHM) of the spin-transition resonance that is below 200 mHz. This is more than ten times narrower than in our previous antiproton magnetic moment measurements⁸. We show that the FWHM is, at present, limited by decoherence induced by cyclotron frequency measurement noise. This is a crucial step towards improved measurements of the p and (bar{p}) magnetic moments with a fractional accuracy less than 100 ppt and will allow for searches of time signatures of asymmetric antimatter/dark matter coupling²³ at improved mblock resolution and increased data-taking rate, thanks to the higher signal-to-noise ratio and smaller FWHM of the coherent measurements.

The heart of our experiment is a superconducting solenoid magnet with a horizontal bore, operated at a magnetic field of B_0,PT = 1.945 T. Inside the bore, the cryogenic multi-Penning-trap system, shown in Fig. 1, is mounted. Most important for this study are the AT, in which the continuous Stern–Gerlach effect is applied¹⁹, the homogeneous PT, in which precision frequency measurements take place, and a park trap (PKT). AT and PT centres are separated by 73.4 mm and PT and PKT centres are separated by 18.6 mm. The trap stack is placed inside a cylindrical hermetically sealed, pinched, cryo-pumped vacuum chamber, in which pressures less than 10⁻¹⁸ mbar and (anti)particle storage times of years are achieved²⁴. The trap electrodes, designed as in ref. ²⁵, are primarily made out of gold-plated copper. The central ring electrode of the AT is made of ferromagnetic CoFe, also gold-plated, which distorts the magnetic field in the centre of the trap to B_AT(z) = B_0,AT + B_2,AT × (z − z_AT,0)², in which B_0,AT = 1.231 T, B_2,AT = 266(5) kT m⁻² and z_AT,0 is the trap centre (Fig. 1a). The magnetic field in the centre of the PT is B_PT(z) = B_0,PT + B_1,PT × (z − z_PT,0) + B_2,PT × (z − z_PT,0)², with z_PT,0 being the centre of the trap. Achieved with a local persistent magnet system, the coefficient B_2,PT can be tuned in a range of about ±350 mT m⁻². The gradient field B_1,PT can be adjusted in a range between 10 mT m⁻¹ and 24 mT m⁻¹. Also part of the magnet system is a set of self-shielding solenoids^26,27, with a shielding factor greater than 50. The trap electrodes are biased with ultrastable voltage sources. The applied voltages are selected such that, in the trap centres, homogeneous quadrupolar potentials Φ(z, ρ) = V₀C₂(z² − ρ²/2) are formed²⁵. Here V₀ is the voltage applied to the central ring electrode, C₂ is a geometry coefficient (Extended Data Table 1 and Methods) and z and ρ are cylindrical coordinates, for which z points along the magnetic field axis. A single particle in such crossed static fields oscillates at three independent frequencies²⁸, at the modified cyclotron frequency ν_+,PT ≈ 29.645 MHz, the axial frequency ν_z,PT ≈ 637 kHz and the magnetron frequency ν_−,PT ≈ 7 kHz. An invariance theorem ({nu }_{{rm{c}}}^{2}={nu }_{+}^{2}+{nu }_{z}^{2}+{nu }_{-}^{2}) (ref. ²⁸) relates the free cyclotron frequency ν_c = (qB₀)/(2πm) to ν₊, ν_z and ν₋; here q and m are the charge and the mblock of the single trapped particle, respectively. Details on the eigenfrequencies and their measurements using non-destructive detection (see Fig. 1b) are described in Methods and summarized in Extended Data Tables 1 and 2.

To implement the coherent spin transition spectroscopy, we use the two-particles/three-traps technique described in ref. ⁸. The measurement protocol is shown in Fig. 2. First, we initialize the spin state of a cold ‘Larmor’ particle in the AT. A second antiproton, the ‘cyclotron’ particle, is prepared in the PT for high-precision ν_c,PT measurements to determine the magnetic field of the trap²⁹. After initialization, the Larmor particle is transported to the PT, at which a spin-flip drive is applied. The particle is then returned to the AT to determine whether a spin transition has occurred.

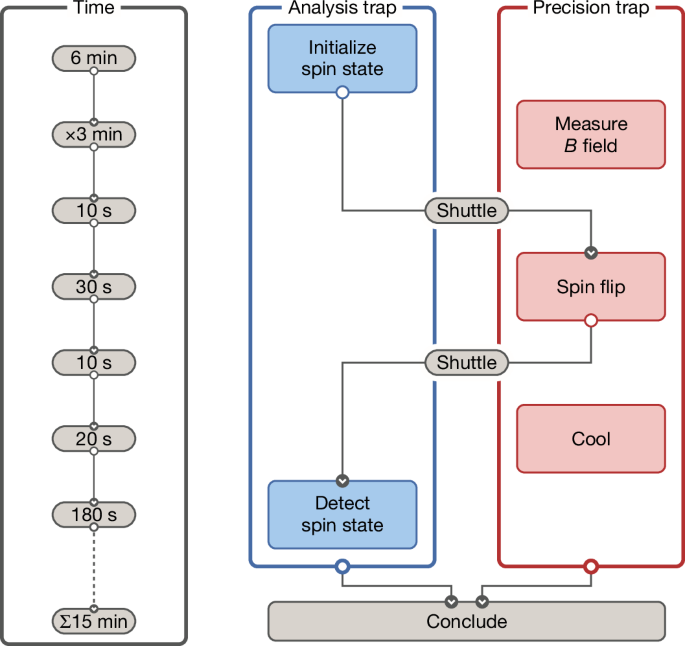
Illustration of the experiment sequence described in the text.

To begin, we first use the magnetic shimming system (Fig. 1a,c) and use measurements with the cyclotron particle to tune the magnetic coefficient B_2,PT. In the case of finite B_2,PT, interaction of the particle with the axial detector causes axial rms-amplitude fluctuations (propto ({k}_{{rm{B}}}{T}_{z}/)(m{omega }_{z}^{2})). These shift the Larmor frequency by ({Delta nu }_{{rm{L}}}=(1/{4{rm{pi }}}^{2})({nu }_{{rm{L}}}/{nu }_{z}^{2})({B}_{2}/{B}_{0})({k}_{{rm{B}}}{T}_{z}/m)) with the particle-to-detector correlation time of about 100 ms, causing motional spin decoherence. We thus tune B_2,PT = 1.2(1.8) mT m⁻², corresponding at the temperature T_z,PT = 8.5(3) K of the PT axial detector to spin coherence times longer than 1 h (ref. ²⁸). Next, we apply the cooling protocol described in ref. ²² to the Larmor particle and cool it to a cyclotron energy E₊/k_B = T₊ < 100 mK. Owing to the presence of the strong magnetic bottle B_2,AT, a spin transition induces an axial frequency shift of Δν_z,SF = 173(1) mHz (ref. ¹⁹). A sequence of axial frequency measurements ν_z,AT interleaved by spin transitions is shown in Fig. 1d.

To initialize the spin state of the Larmor particle, we apply a sequence of ν_z,AT measurements, each taking 120 s, followed by a 10 s injection of a magnetic spin-flip drive at ν_rf,AT = 51.651 MHz. At the background ν_z,AT scatter¹⁰ Ξ_back,AT ≈ 32(2) mHz achieved in this trap, we identify a measured ν_z,AT difference Δν_z,SF > 140 mHz as a spin transition. This leads to spin-state initialization with a confidence of about 100%. Subsequently, we use the cyclotron particle in the PT to determine B_0,PT in this trap. To that end, we measure ν_c,PT, using the technique described in ref. ²⁹. A single cyclotron frequency measurement of approximately 180 s resolves ν_c with a fractional uncertainty of σ(ν_c,PT)/ν_c,PT = 1.42(7) ppb. This frequency defines the radiofrequency that is irradiated to later induce the coherent spin transitions in the PT ν_rf,SF,PT = (g_p/2) × ν_c,PT, in which g_p/2 = 2.7928473441 is used⁸. Next, we move the cyclotron particle to the PKT centre and the Larmor particle from the AT to the PT, by applying voltage ramps to the transport electrodes that interconnect the traps. Then a spin-flip drive at ν_rf,PT is irradiated for a time t_SF,PT, transmitted by a coil mounted close to the PT (Fig. 1a). Afterwards, we move the Larmor particle back to the AT and the cyclotron particle to the PT and cool its magnetron mode. To identify whether the spin in the PT was flipped, we record a subsequent ν_z,AT/spin flip sequence to compare the spin state in which the particle was leaving the AT and once it returns from the PT. Here we identify a measured ν_z jump of Δν_z > Δν_z,SF/2 = 0.173/2 Hz as a detected spin transition²¹. The error rate of identifying the spin flips driven in the PT depends on the axial frequency scatter of the ν_z,AT sequences; the formalism to correctly estimate the error rate is described in refs. ^30,31. The median axial frequency scatter of 32(2) mHz corresponds to an error rate less than 5%.

By applying this protocol and adjusting the radiofrequency interrogation time t_SF,PT to drive spin transitions in the PT, we repeat the procedure 20 times for each value of t_SF,PT, thereby obtaining the spin-flip probability P(t_SF,PT), shown as the blue data points in Fig. 3. This corresponds to the first observation of Rabi oscillations with a single nuclear spin 1/2 antiparticle. The red line is a Monte Carlo fit (Methods and Extended Data Table 3) of

in which the function

is the spin-flip probability with Rabi frequency Ω₀, detuning Δ = ν_rf,PT − ν_L and interrogation time t. The function G(µ, σ) is a Gaussian distribution, defined by the scatter σ ≈ 52 mHz, arising from the ν_c,PT measurement noise present during these experiments. This noise leads to an observed decay of spin inversion, to which an effective spin coherence time of τ_s,PT = 50.2(4.8) s can be blockigned. For further details on the blockysis, see Methods. This indicates that, in an optimized Rabi resonance scan, executed on the π-pulse, a FWHM Δν_FWHM ≈ 20 mHz or 250 ppt could be achieved. We note that magnetic noise imposed by the accelerator reduces the spin coherence time to 5.6(4) s (Extended Data Fig. 1).

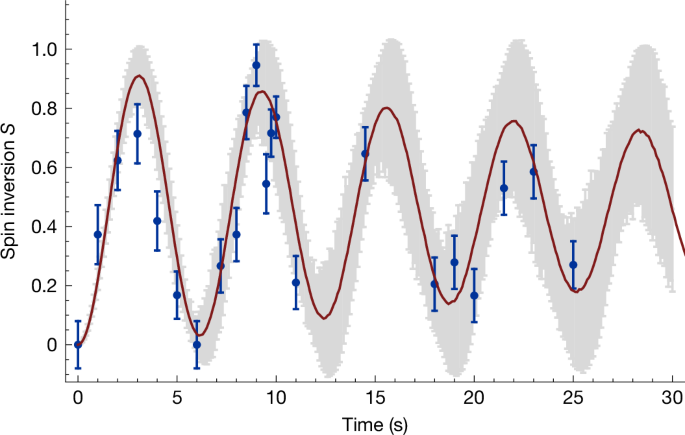
Observation of coherent Rabi oscillations of the spin of a single trapped antiproton. The blue points represent the measured data and the red line depicts a Monte Carlo fit, which blockumes 52 mHz cyclotron frequency measurement decoherence as determined in the related measurements. In grey are the uncertainties of the Monte Carlo simulation. The effective coherence time is τ_s,PT = 50.2(4) s. Each point is an average of 20 spin flip attempts, uncertainty bars represent the standard deviations of the measured data distributions. Throughout the measurement campaign we have recorded several of these plots for different Rabi frequencies.

To optimize the spectral response of the coherent dynamics for measurements at optimum line-centre resolution, we first record Rabi oscillations at different drive amplitudes and determine the t_SF,PT in the PT at which maximum inversion is achieved. At the determined optimum t_SF,PT, we perform Larmor resonance scans, keeping t_SF,PT constant while scanning the frequency ν_rf,PT of the spin-flip drive with respect to ν_L = (g/2) × ν_c,PT. Here ν_c,PT is obtained with the cyclotron particle in the PT, extracted from a sequence of six frequency measurements, taken before the application of the spin-flip drive. To resolve the resonance, we sample ten points per irradiated ν_rf,PT and scan each resonance with a minimum amount of eight discrete frequency offsets, which typically takes 60 h. The recorded cyclotron frequency sequence allows us to study Δν_FWHM and the inversion S as a function of ν_c,PT averages used to reconstruct ν_L at the time when the spin-flip drive is applied in the PT. Averaging several magnetic field measurements for the ν_L reconstruction decreases the cyclotron frequency scatter σ_c,PT to about 30 mHz, which narrows the width of the Larmor resonance while increasing the inversion. This is shown in Fig. 4a, in which we plot the ratio of inversion S ∈ [0, 1] over the measured Δν_FWHM as a function of the Rabi frequency Ω₀/(2π) applied to sampled spin resonances. The purple data points are for one ν_c,PT measurement and the blue points are for four averages that are used to extrapolate ν_L. The grey lines represent the calculated scalings for different cyclotron frequency fluctuations between σ = 30 and 100 mHz. More than four ν_c,PT averages, due to a random walk in the field of the superconducting magnet, adds further fluctuation, broadening the Larmor resonance line again.

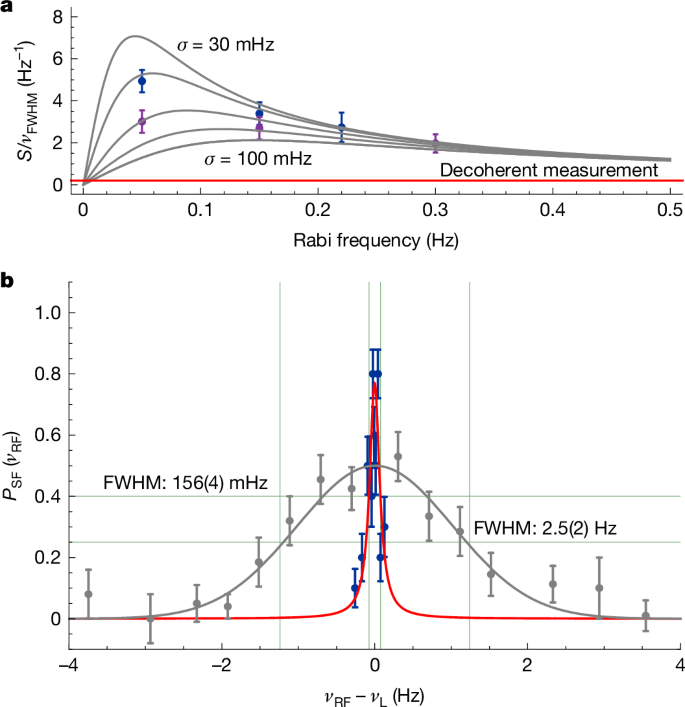
a, Signal S/Δν_FWHM for different Rabi frequencies and σ_c,PT. The grey lines are calculated results for σ_c,PT = 30, 40, 60, 80 and 100 mHz. b, Measured coherent ν_L resonance at the optimized parameters found in the experiment, blue scatters and best least-squares fit of a Voigt profile to the data (solid red line). The grey data points are from the previously measured antiproton g-factor resonance⁸. The coherent line has 1.54 times higher signal-to-noise ratio and a FWHM (green vertical lines) that is about 16 times narrower than the width in ref. ⁸. For both plots, the uncertainty bars represent the standard deviations of the measured data distributions.

By systematically scanning the interrogation times and Rabi frequencies, we obtain at Ω₀/(2π) ≈ 50 mHz and a drive time of 16 s a signal inversion of 0.77(4) at Δν_FWHM = 156(4) mHz, as shown in Fig. 4b. The blue data points represent the measurement described here and the red line is a fit of a Voigt profile. Compared with the previous most precise measurement of the antiproton magnetic moment⁸ (grey data in Fig. 4b), this corresponds to an increase of the inversion by a factor of 1.54 at a 16-fold reduction of the FWHM of the resonance line. The line-centre determination of the dataset is at a level of 12 mHz or 150 ppt statistical uncertainty, ten times more accurate than in ref. ⁸. Note that this resonance was sampled during a data-taking period of only about 60 h, whereas the data ac***ulation in our previous measurement took place over a period of two months.

The statistical uncertainty in determining the line centre of such g-factor resonances scales proportionally to Δν_FWHM/S. Consequently, on the basis of our coherent spin spectroscopy data, we infer that, under present experimental conditions—relative to those reported in ref. ⁸—an approximately 25-fold improvement in the statistical precision of the g-factor line-centre determination is achievable. However, the two-particle method introduces systematic limitations on the interpretation of the measured line centre. Specifically, the transfer of particles between the AT and the PT induces magnetic field variations and voltage settling drifts. These effects undermine the critical blockumption that the magnetic field remains constant between the ν_c,PT measurements and the application of the Larmor drive—a requirement for the precise determination of the antiproton magnetic moment. Quantifying the complete systematic uncertainty budget within the limited three-month annual shutdown of the accelerator remains a substantial challenge. Because accelerator operation reduces the spin coherence time by nearly an order of magnitude, systematic shifts during on and off periods differ. Although using a single-particle double-trap technique²¹ could mitigate the present systematic uncertainties, this approach would substantially extend the required data acquisition time—beyond what is feasible during the short shutdown windows. To address these limitations, we have developed the transportable antiproton trap BASE-STEP³², enabling the relocation of antiprotons to dedicated, quiet laboratory environments at HHU Düsseldorf and CERN. These facilities will host precision experiments not exposed to accelerator-induced magnetic field fluctuations. By combining coherent spin quantum spectroscopy with phase-coherent cyclotron frequency measurements in such an environment, it will become feasible to suppress magnetic field noise by at least a factor of five. This would allow statistical resolutions of the g-factor line centre at the level of approximately 10 ppt. The application of these techniques to the proton would open the path towards one of the most stringent tests of CPT invariance in the baryon sector¹².